実際に本年度の東京大学の数学の入試問題を解いた東大生チームが、今年度のキーポイントや、そこから見えてくる出題者の意図について、数学的側面を全面に押し出して解説します。
まず、私達が解いた所感では、6つの大問の難易度は以下の通りです、Aが簡単でDが難しい問題です。
(また、難易度はそのセット内での相対的な難易度としています。)
- 第1問:A
- 第2問:B
- 第3問:B
- 第4問:C
- 第5問:D
- 第6問:C
以上より、解きやすさの順番とすれば、
第1問>第3問≧第2問>第4問≧第6問>第5問
といった順番でしょう。難しい大問の中にも取りやすい小問は散見されましたので、依然として東大数学においては、「完答だけにこだわらず、解ける部分を確実に解く」という戦略が有効だったと言えるでしょう。
粘り強さを問うている問題
まず、問題の全体感をみたところ「6個あるどの問題も、完答するには骨が折れそうだ」と感じました。
ここで、「完答」とは、その大問を完全に解き切ること(=最後の小問で問われている値を求めたり、最後まで論証を完遂すること)を指す受験用語です。
今回の東京大学理系数学は、どの問題も重厚で、解き切るために相当の労力を要しました。
ですから、数学が苦手な受験生の中には、全く手も足も出なかったという人も居たのではないかと推察されます。
そんな2025年度東大理系数学で一番平易だったと思われるのは、大問1のこの問題。

今年出題された6問のうち、最も発想力を必要とせず、問題で問われていることもシンプルなので、この問題はどうにかして完答したいところです。
しかし、そんな問題でも一筋縄でいかないのが、本年度の東大。
(1)で求めさせられている点Utの座標は絶対に間違えられないプレッシャーの中、煩雑な計算を丁寧に実行することが求められますし、この大問内で比較的簡単な(2)でさえも媒介変数表示の積分を計算する必要があります。また、最後の(3)では、この式の左側を見て、右のように2乗の形に変形し、ルートを外せることを見抜けなければ、計算を進めることができないという、数学的なセンスも要求されます。
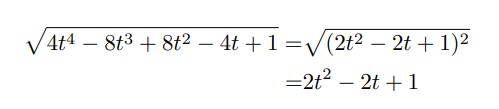
計算過程で手が止まってしまったとしても「2乗の形を作り出してルートは外せるはずだ!」と粘り強く考えて、ようやく完答できるという訳です。
このように、今回の入試問題にはいくつかの問題で「こうならないとおかしい。」「こう計算できるはずだ。」と、あたりをつけて解き進めるという数学的な能力も要求されています。
実は、大学以降で数学を学ぶ際にも、このようなあたりを付けることは重要です。
というのも、抽象度の高い内容を定式化するにあたっては、自分の中にある「なんとなく、こうなりそうだな」というイメージを、誰もが理解できる数式に落とし込むことが求められ、そのために、自分の直感から導き出した答えから、あえて逆算して論理を組み立て、そこから議論を展開することも多いのです。
ちなみに、大問1は、ベクトル・媒介変数表示の積分・曲線の長さ、といった中々入試問題で扱われないトピックを浅く広く扱っている問題であり、問題の完成度の高さも相まって、ここ20年の中でも屈指の良問と言えるでしょう。
なお、京大理系数学2019の大問3に類題が出題されています。こちらは誘導が無い分、方針を自分で設定しなければなりません。これらの問題を並べるだけでも、東大と京大の出題形式の違いが垣間みえて面白いでしょう。
粘り強さと数学力を問うている問題
粘り強さを問うている問題は他にもありました。
それが、この大問3です。
この問題は、大問1に続いて取り組みやすい問題であり、数学が極端に苦手な受験生以外は完答したいところです。

ただ、第1問と同様に、完答するとなると相当の数学力が要求されます。
この問題の難しいポイントは以下の2つです。
- 計算を丁寧に実行した上で、得られた結果を見て、「三角関数の合成を用いて最大値を求める」という発想が浮かぶか。
- 問題の最後に潜む、「場合分け」に気付けるか。
まず、①の、「三角関数の合成を使う」という部分に気づけなかった受験生も多いかもしれません。三角関数の合成を使うには、「角度が揃っている」ことが必要なのですが、そもそも面積Sを求めるまでの計算も少し面倒で、その過程で一箇所でも計算ミスをしてしまうと、Sを計算した後に「角度が揃っているな」とは思えず、そうなると、結果的に後の小問まで総崩れする可能性があるという点で、数学力が要求されたポイントでした。
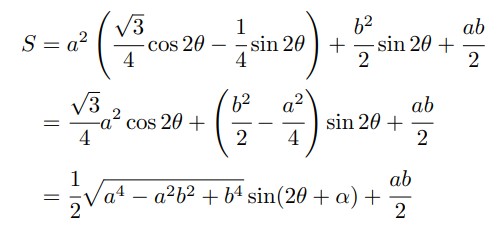

(なお、さらに数学力を高めたい人は、より綺麗な形で三角関数の合成を行うことを考えてみましょう。後の場合分けの計算が少し簡単になります。)
そして、その関門を越えた後、さらに自力で「場合分け」に気づく、というのが難しいのです。
また、場合分けがありそうだと気付いたとしても、三角関数の合成をした後に出てくる値がやや煩雑な形をしているため、具体的にどのような場合分けを行えば良いのか、というところまで求めることは至難の技です。
総じて第3問では、多少煩雑な計算であっても自分の計算力を信じて突き進み、論証部分も丁寧に対処する、という純粋な数学力の高さが問われていたと言えるでしょう。
その他の問題と全体の所感
その他の問題にも少しずつ触れておきます。
大問2は、(1)だけ見れば全体の中で、群を抜いて平易な問題のため、東大受験生として落とすことは許されない問題です。しかし、(2)に関しては、これまた一筋縄ではいかない問題でした。まず、極限と積分が絡む問題ですから、「はさみうちの原理を使うはずだ!」と思えることが大事です。その後も、うまく極限を計算したり、下からのはさみ方をどうするか考えなければならない点が難しかったと言えるでしょう。
全体として、大問1,3に次いだ難易度の問題ではあることは事実なので、数学が得意な人であれば完答を狙いたい問題です。
なお、logの凸性(イェンゼンの不等式)を利用したり、相加相乗を利用したり、部分積分で計算を実行したりと、誘導に乗らずとも多彩な解法が想定される問題でした。
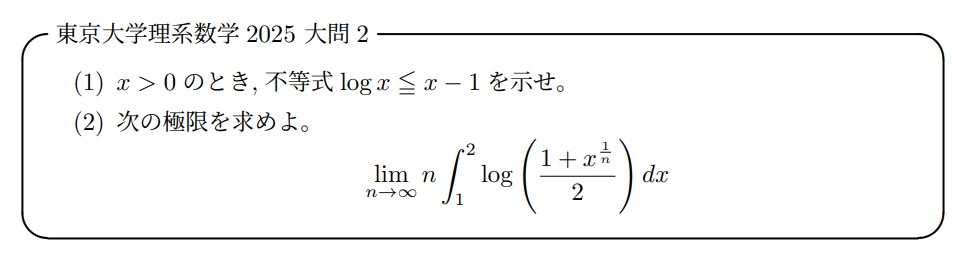
大問4は、(1)は比較的解きやすいため、数学が得意な人であれば解きたい問題です。「直接示すことが難しそうであれば、対偶を示す。」というオーソドックスな発想ができるかどうか、基礎力が問われた問題と言えるでしょう。(2)も、整数問題に慣れていれば方針自体は立ちやすかったと思いますが、論証が難しく、試験会場では捨て問気味の問題です。方針だけ解答に記載し、撤退するのも勇気です。

大問5は、目新しい設定ではありますが、(1)の論証は頑張りたいところ。様々な論証方法がありますから、採点に際しても広く門戸が開かれているでしょう。自分の思考を答案に乗せる技術が問われた問題と言えます。
目新しい設定で自分の考えを答案に載せる力が問われるような問題は、直近では東大理系2020大問1、東大理系2016大問5、東大理系2015大問5 などで出題例があります。
また、(2)の方針自体は、定石である「場合の数の漸化式は、最初の1手で場合分け」を使えると考えられるでしょう。しかし、方針に気づいてもなお定式化が難しく、筆者個人としては、本年度の最難問だと思います。

大問6は、高校数学で習った知識をフル活用するような問題で、これまた数学力が試される良問かつ難問です。具体的には、複素数平面、軌跡・領域、二次曲線、といった分野を横断している問題で、問題集に載っている類題も少ないことから、試験会場で解ききれた受験生は少ないことでしょう。
なお、最近出題された問題の中で一番内容が近かったのは、東大理系2018の大問5です。

総合して今年度は、直近10年で最難と言われていた2022と同程度の難易度であると考えられます。
また、昨年度は東大数学の採点の厳しさが話題となりましたが、今年度は問題自体が難しくなっているので、採点基準に関してはある程度甘くなりそうだと考えられます。
それでも、全体として点数を稼ぎづらいことには変わらず、生半可な数学力では太刀打ちできないセットであったことは間違いないでしょう。
2018年以降、東大入試は重厚な問題が多くなっており、それに付随して、総合的な数学力や受験生の粘り強さ求められるようになっています。「方針が明確で計算量も少ない」という問題は、ほとんど出題されないと言って良いでしょう。普段の勉強に際しても、模範解答を見て覚えるだけの勉強に終始せず、問題の本質を捉えるように心がけてください。


















