皆さんこんにちは!
現役東大生、「#計算の申し子」の永田耕作です。
前回、100マス計算についての記事を書かせていただきました。多くの方に読んでいただいているようで、とても嬉しく思っております。今回の記事はこの続編になるので、まだ読んでいない方は、ぜひこちらの記事を先にお読みください!

逆100マス計算とは?
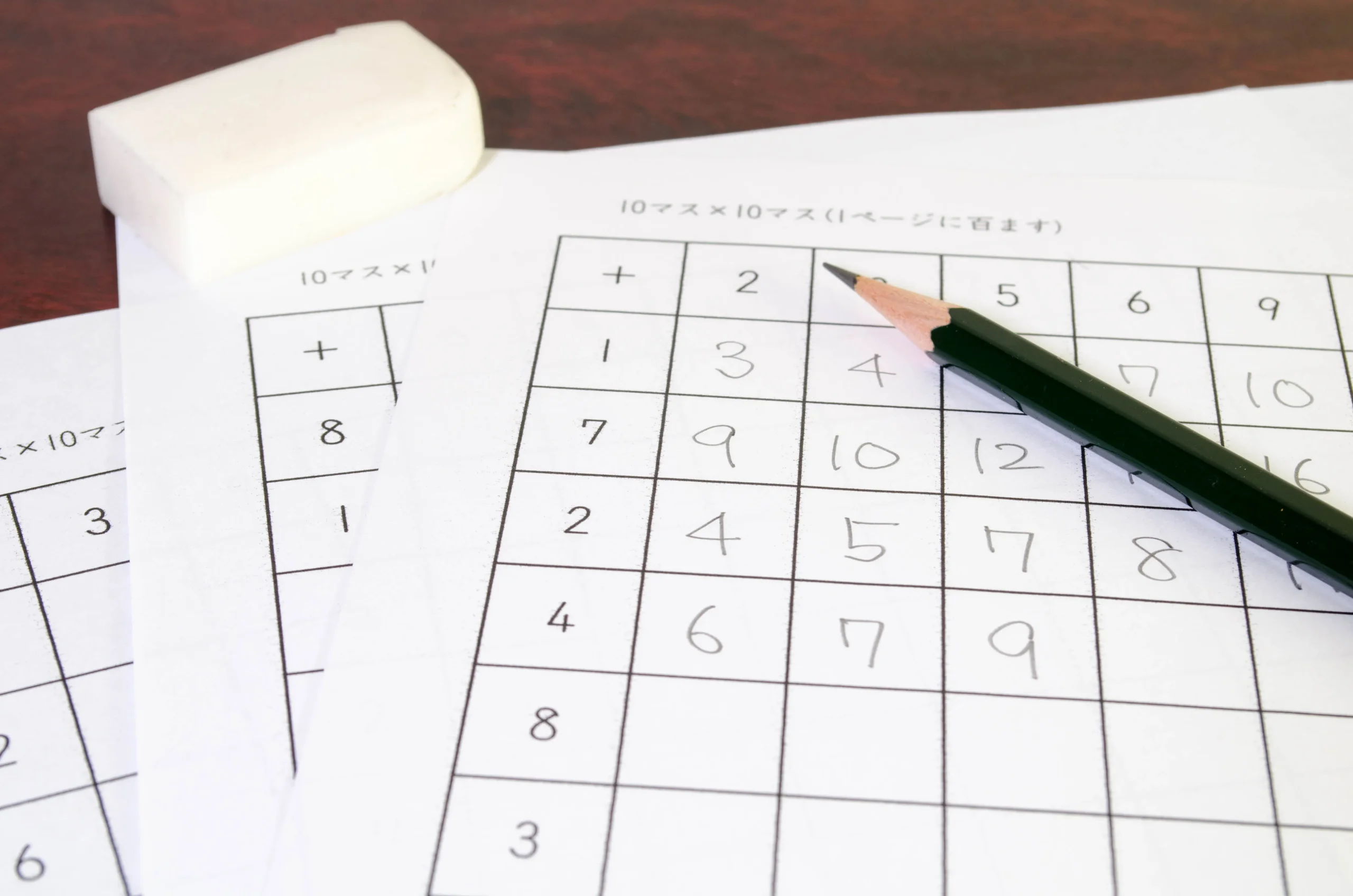
さて、今回は一体どんな100マス計算をやっていくのか。実は、「逆100マス計算」という面白いものを僕は見つけてしまったのです。まずはこちらをご覧ください。
皆さんはこれを見てどう思いますか?
100マス計算と形式は同じですが、違う点がありますよね。
この逆100マス計算は、すでに埋まっている足し算の計算結果から、一番左の列にある「たす数」と、一番上の行にある「たされる数」を逆算して求めていく問題です。
今回であれば、「たす数」「たされる数」はそれぞれ1から10までの数字が1つずつ入ることになります。
実際に例を挙げて解き方を説明すると、
一番上の段の左から2番目にある「16」という数字から
「じゃあたす数が7、たされる数が9になるんじゃないか?」
「たす数もたされる数も両方8になるかもしれない」
などの検討を行いながら解き進めていくことになります。
通常の100マス計算は「7+9」を計算して「16」にするのに対して、逆100マス計算は「⚪︎+△ = 16」から⚪︎と△がいくつになるかを考える計算になるため、逆100マス計算の方がレベルは上がります。
この逆100マス計算、慣れていない人はかなり時間がかかってしまうと思います。僕も時間を測って実際にやってみたのですが、通常の100マス計算よりも手こずってしまい、3分20秒もかかってしまいました。
しかし、周りの理系東大生のメンバーにやってもらったところ、なんと30秒で解き切った猛者がいました。これは驚きのタイムですよね。
素早く解くことができたメンバーに話を聞いてみると、どうやら3つのポイントがあることが分かりました。これにいかに早く気づけるかが勝負のカギになるのです。
逆100マス計算を解く3つのポイント
ポイントについて具体例も挙げつつ解説していきます!
①「2」を探す
②まず1行を埋める
③四角形を見つける
①「2」を探す
僕はこの記事を執筆するにあたって、実際に10人程度の弊社にいる東大生にこの「逆100マス計算」を解いてもらったのですが、そのメンバーがみんな口を揃えて話していたのは、
「いかに最初に『2』に着目できるかが重要だ」
ということでした。この「2」という数字は、上から3行目の一番左の列にあるすでに埋まっているマスのことを指します。なぜここで「2」が重要になるかというと、答えはシンプルで、「2」がある時点で「たす数」も「たされる数」も「1」であることが確定するからです。
冒頭で述べたルールの通り、たす数もたされる数も1から10までの数字が一つずつ入ります。つまり、足し算の結果でマスに入る数の最小値は「1+1=2」より「2」、最大値は「10+10=20」より「20」となります。この最小値である「2」が埋まっているということは、必ず1+1の足し算が行われていると決定づけられるのです。
多くの人は気づいていると思いますが、この逆100マス計算を短い時間で行うためには、「たす数」と「たされる数」をいかに早く埋められるかがカギになります。理由はシンプルで、そこが埋まった時点であとは通常通りの100マス計算に早変わりするからです。この「たす数」「たされる数」を埋める上で重要になるのが、「2」のマスの存在なのですね。
「2」を見つけてたす数、たされる数それぞれ「1」を埋めることができれば、あとはその「1」がある行、列それぞれのマスを埋めていくことができます。例えば、たす数の上から3番目が「1」と分かることで、その行のすでに埋まっている数字(左から「3」「10」「8」)と照らし合わせて、たされる数の左から6番目が「2」、8番目が「9」、9番目が「7」というふうに数字が埋まっていきます。ここで、埋まった左から6番目の「2」を利用してたす数の1番上が「8」、4番目が「2」というふうに、五月雨式に数字が埋まっていくのです。このように考えると、最初に「たす数」「たされる数」の「1」を埋めることがいかに重要か分かっていただけたでしょう。
②まず1行を埋める
ここまでの説明を受けて、このように考えた人もいるのではないでしょうか?
「なんだ、2に気付けなかったら解けない、ってことか」
気持ちは分かります。でも、東大生のすごいところは、このようなひらめきがなくても確実に最適な方法を見つけて問題を解き進めることができるところなのです。
僕がこの問題を解いてもらった東大生の中にも、「2」を見つけるという発想が最初に浮かばなかった人は何人かいました。その人はどうしたのかというと、それぞれの行、列を観察し、どこの行、列にあらかじめ多くの数字が埋まっているのかを確認したのです。今回の問題で言えば、例えば上から2行目、横から5列目などがそれぞれ4つずつ数字が埋まっている場所、いわば「ホットスポット」になります。このようなヒントの多い場所に着目して問題を効率的に進めようと工夫しているのです。
実際にこの問題を解いた理系の東大生は、このように語っていました。
「上から2行目ですでに埋まっている数字に着目すると、左から3番目〜5番目のマスに埋まっている数字が7,8,9と連続していることがわかった。つまりここから、たされる数の左から3番目〜5番目のマスに入る数字は連番であることがわかる。これを応用すると、上から4番目、左から3番目のマスに6が入っていることから、その右隣は7,8と続くことがわかる。このようにして、左から3番目〜5番目の列の数字を埋めていくことができる。」
とても堅実な数字の埋め方だと僕は考えます。ひらめきに頼らなくても、このようにできる場所から埋めていくことで答えに辿り着くことができるのです。
③四角形を見つける
もう一つ、面白い視点を用いてこの逆100マス計算を解いている東大生がいたので、最後にその例を共有しようと思います。それは、「四角形を見つけて数字を埋める」という方法論です。
この画像の赤い丸がついた4つの数字を見てください。10,4,18,12で大きな四角形を作れることがわかります。ここで興味深いのは、10,4の数字の差と18,12の数字の差が「6」で等しくなっていることです。同様に、縦で数字を見た場合の10,18の数字の差と4,12の数字の差も「8」で等しくなっています。このように、4つの数字を見るとその関係性を浮かび上がらせることができるのです。
これを応用すると、数字を埋めていくことができるのです。青い丸がついた4つのマスを見ると、6と5の数字の差から、数字が埋まっていないマスに入る数字は
14 – 1 = 13
であることが分かります。この数字の埋め方は効率の良いやり方ではないかもしれませんが、確実にゴールに近づくことができる方法だと言えるでしょう。
最後に
100マス計算はゲームのようなものに見えて、計算力を高めてくれる勉強に役立つ優れものです。小中学生はもちろん、大人になってもその効果は絶大です。
今回は、その100マス計算に一捻りを加えた「逆100マス計算」に着目し、色んな解き方を紹介していきました。問題の解き方は人それぞれなので、自分に合った解き方を見つけてみてほしいと思います。
ちなみに、100マス計算の特殊型は僕も驚くくらい多くの種類がありました。全部制覇すれば計算力をグッと高めることができるので、ぜひ皆さんも調べてみてください!
今回の記事は、こちらで以上となります。また次回の記事でお会いしましょう。
公式サイトにて、カルぺ・ディエムが提供している具体的なサービスを紹介中!
カルペ・ディエムでは、学校や保護者のみなさまが抱える懸念やニーズに応える形で、講演・講座・ワークショップを提案し、それらを実施しております。
生徒の皆さんの大学選びや学部選びのワークショップ、モチベーション向上を目的とした講演、独自の探究学習授業、長期休暇中の学習合宿、難関大学合格を目指した通年プロジェクトなど、さまざまなプランをご用意しております。
私たちの講師は現役東大生で 偏差値35から東大合格を果たした西岡壱誠をはじめ、地域格差や経済格差などの多様な逆境を乗り越えた講師たちが、生徒の皆さんに寄り添って全力でサポートいたします。
ご質問やご相談だけでも結構ですので、お気軽にお問い合わせください。