東大経済学部生が競馬に1万円賭けたらどうなるのか　アカデミックマインドを用いて考えてみる

今回は競馬を知らない東大経済学部生がさまざまな手法で競馬を分析し、実際に1万円を賭けてみるといくらになるのか、観察します。その手法や再現性に注目し、ぜひ最後までご覧ください。

競馬で勝つ方法を考えてみよう

期待値を用いて判断してみる

単勝について

競馬を実施する上で、期待値の計算を参考にしてみたいと思います。期待値とは、リターン額とその確率の積であらわされます。競馬においては、リターン額は購入金額にオッズをかけるた額から掛け金を引くことで算出できますが、勝率をどのように計算するのが良いでしょうか。

サイコロのような場合、ある目が出る確率はイカサマをしない限り等しいはずです。これを競馬に応用した場合、10頭立てレースであればある馬が勝つ確率は等しく1/10となるはずです。このような場合は10倍以上のオッズのものをかければ勝機があるということになります。しかしこれは正しいでしょうか。

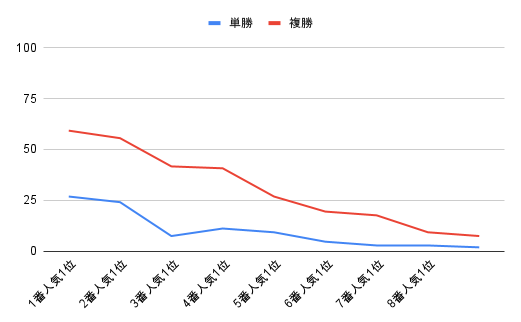
ここでは過去のJRA競馬の人気順と、各人気順に対応する勝率を求めてみます。東京競馬の過去100レースの単勝について、人気順と勝率を求めると以下のようになりました。

1番人気	約27％
2番人気	約24％
3番人気	約7%
4番人気	約11％
5番人気	約9％
6番人気	約3％
7番人気	約3%
8番人気	約1%

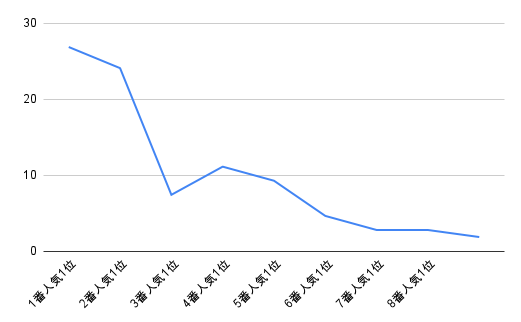
ただし、このデータは出走頭数によらず集めているため、やや不適切です。特に16番人気などはそもそもの数が少ないため、全レース数で割った率も低くなります。しかし最低でも3頭以上は出頭していることから、本記事では1〜3番人気までの傾向を調べます。なお対象期間の最低出走頭数は8頭であり、単純な確率であれば12.5％となるため、人気順と勝率の高さには有意な関係があると言えるでしょう。

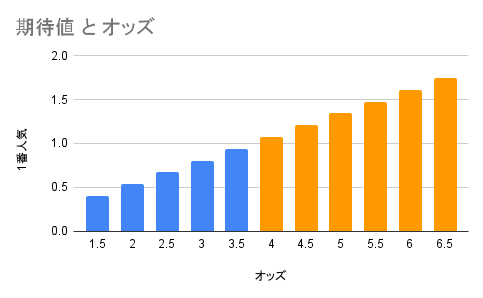
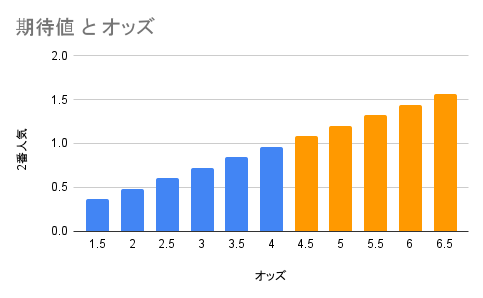
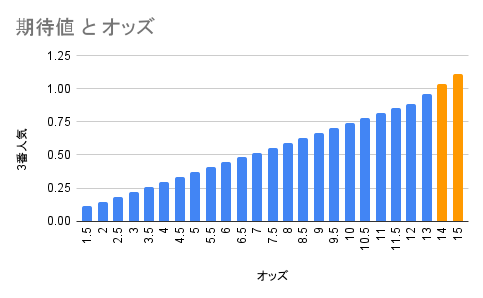
一番人気の勝率27％に、オッズをかけた数値が掛け金を超えれば、何度も試行した結果として収支がプラスになるであろうということになります。より一般化し、割合で考え、以下の表にまとめました。

オレンジ色で表示した部分は期待値が1を上回るため、このオッズ以上であればかけよう、という判断基準になります。

探究1
問い「競馬で勝率を計算するためにはどうすれば良いのか」
⇩
仮説「オッズに着目するとある程度一定の傾向が見えるのではないか」
⇩
検証「JRAサイトから情報を収集し、勝率を推定する」

参考：複勝の場合

複勝の場合、参考にした全108レース中、64レース（59%）において1番人気の複勝が的中していました。すなわち、こちらも期待値を参考にすれば、複勝オッズが1.7倍を超えていた場合は勝つ可能性が高いということです。なお2番人気は56%、三番人気は42%でした。単勝と比べると勝率はかなり高いです。

1番人気	約59％
2番人気	約56％
3番人気	約42%
4番人気	約41％
5番人気	約27％
6番人気	約19％
7番人気	約18%
8番人気	約9%

ポートフォリオを使った分析

次に他の投資対象と、競馬における平均リターンと標準偏差を、国内株式投資の平均リターンと標準偏差と比較してみました。競馬においては一番人気の単勝のみを購入するとし、的中確率は過去データより27％、オッズは平均3.0倍として計算します。この場合、競馬の収益率（平均リターン）は、

0.73*(-1.0)＋0.27*(3.0-1.0)＝-0.19

よって、平均的には19％の損失が生まれます。またこの平均リターンから標準偏差を求めると、標準偏差は177％となりました。

次に国内株式について、GPIF（年金積立金管理運用独立行政法人）が適用する基本ポートフォリオを参考にすると、国内株式の平均リターンは4.8%、標準偏差は19％程度とされています。

これを投資機会集合という手法により分析します。通常、この手法はどの株式をどれだけ保有するのかといった判断に用いられますが、今回はその片方を馬券にしてみます。なお、本来であれば株の標準偏差は正規分布を前提に考えれられますが、馬券においては確率が勝ち負けの両方に偏っているため、厳密には不適切であることをご理解ください。

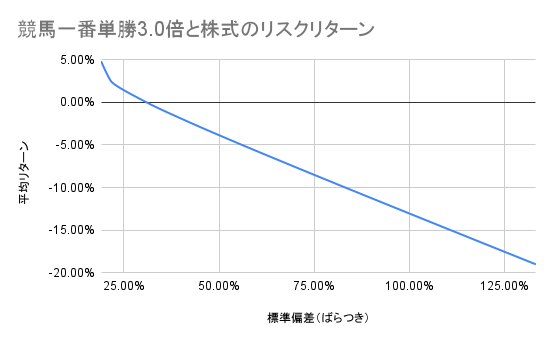
この表では右に行けば行くほど、国内株式に対する馬券の割合が大きくなります。また、横軸はばらつき、縦軸は平均的なリターンの大きさを表します。この場合、馬券の割合を増やせば増やすほど、ばらつき（不安的さ）が大きく、平均リターンが小さくなります。これでは馬券を購入する意義を見出すことができません。期待値が負である馬券の割合を増やせば増やすほど、期待されるリターンが下がっていくのはイメージ通りですね。

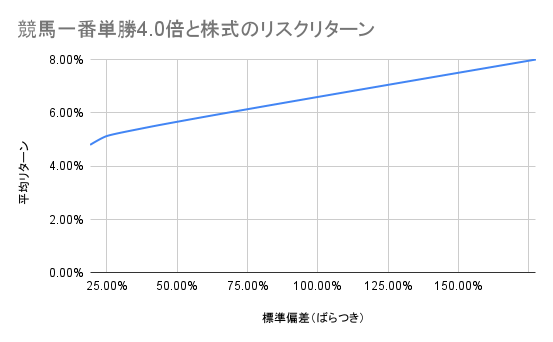
一方、馬券のオッズを4.0倍にしてみると、上向のグラフになりました。しかし、国内株式市場のばらつき（標準偏差）は19％（0.19）なのに対し、馬券の標準偏差（ばらつき）は開始地点でも25%と、かなり大きくなりました。標準偏差の計算において参考にできるデータがあたりかハズレかしかないので仕方ありません。

探究2
問い「株式と馬券の保有割合によるリターンはどう変化するだろうか」
⇩
仮説「株式の方が安定していそうだが、表に表してみるとより見えやすいのではないか」
⇩
検証「馬券を増やせば増やすほど、平均リターンが増える場合があるが、不安定要素が大きすぎる」

以上のような結果から、競馬を投資として捉え勝利を目指すのは、株式投資に比べると非常にリスクが大きい戦いであることがわかりました。競馬なんかせずに大人しく競馬場でモツ煮を食べておく方が良いかもしれませんね。

競馬協会は何で儲けているのか

ここからは少し趣向を変え、業界全体というややマクロな視点から考えてみたいと思います。そもそも、競馬を開催するためには競馬場の維持管理、競走馬の育成、ジョッキーへの賞金など、さまざまな経費がかかるはずです。このお金はどこからきているのでしょうか。

JRAの収支報告書を調べてみると、馬券の売上金から25％は協会が天引きした上で当選者に配当しているとのことでした。すなわち、勝っても負けても、25％は協会のものです。また売上金の10％は国庫に納付される仕組みとなっています。その他に入場料などの収益もありますが、大きなウエイトを占めるのはやはり勝馬投票券の売上のようです。

つまりは、基本的には損をするのがスタートだということです。やはり、儲けに行く場所ではないのかもしれません。しかし、馬が目の前で走っていて、当たるかどうかのワクワクも楽しめるということは、ただお金をかける以上に楽しみがあることのように思います。夢を買っているという点では、ディズ○ーランドと大差ないでしょう。

探究3
問い「なぜ競馬協会は成り立っているのか」
⇩
仮説「競馬協会の収支報告書を見ればわかるのではないか」
⇩
検証「売上金の一部を天引きしていた」

JRA 決算等の情報

馬券の保有割合を考えてみる

先ほど株式投資との保有割合をみてみると、直線的なデータが得られました。ここからは投資対象を馬券に絞り、馬券の保有割合を変えて考えてみましょう。

他の投資対象も同じですが、基本的にはさまざまな投資商品を持ってリスク分散することが鉄則であると言われます。今回はいくつかのパターンで馬券のリスク分散を、先ほどの投資機会集合を用いて考えてみましょう。

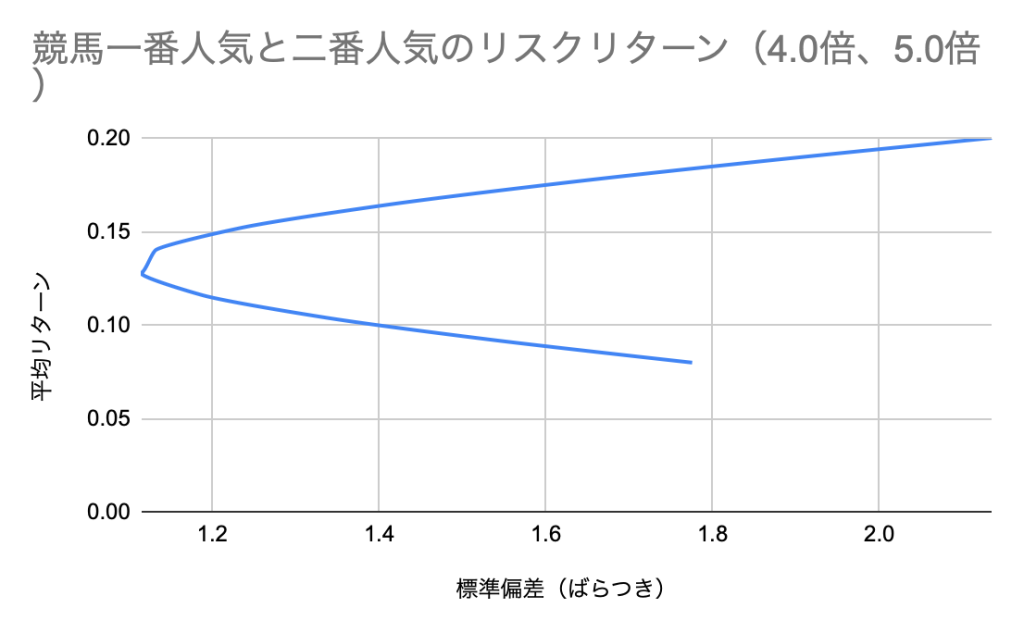
まずは一番人気が3.5倍、二番人気が5倍という場合を考えましょう。

1番人気比率	2番人気比率	期待リターン μP​	標準偏差 σP​
100%	0%	-0.055	1.5539
90%	10%	-0.0305	1.3406
80%	20%	-0.006	1.1682
70%	30%	0.0185	1.057
60%	40%	0.043	1.0269
50%	50%	0.0675	1.0847
40%	60%	0.092	1.218
30%	70%	0.1165	1.4055
20%	80%	0.141	1.6285
10%	90%	0.1655	1.8745
0%	100%	0.2	2.1354

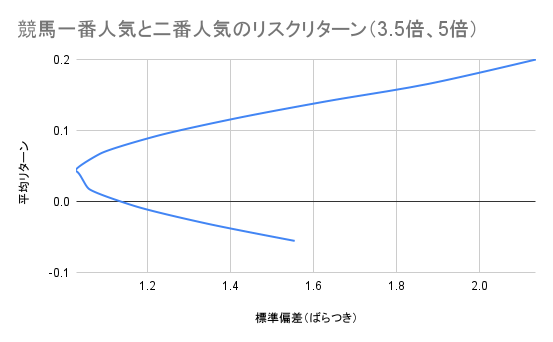
くの字型のグラフが現れました。一度標準偏差が小さくなる場所があるということです。このグラフをみるとわかる通り、くの字の下の部分は、横軸のリスクに対して2通りの平均リターンがあるうち、平均リターンが低い方であることがわかります。このような区間は非効率的であることがわかるでしょう。くの字の上部分が効率的フロンティアと呼ばれ、こちらの範囲内で投資判断が行われると言われています。やはり標準偏差は依然かなりの大きさがありますが、リターンがプラスに転じていることは注目すべきです。二番人気の比率を3/10より大きくすることが必要でしょう。ただし、このグラフの形状及び場所は、オッズによってかなり変動するため、都度競馬場内で計算する必要がありそうです。そしてこの割合によって購入する馬券の金額を変えることとします。

探究4
問い「リスク分散の観点から馬券を複数購入したらどうなるだろうか」
⇩
仮説「合成ポートフォリオで分析してみればわかるはずだ」
⇩
検証「効率的な保有割合が存在することが分かった。ただしオッズにより位置は変動する」

競馬の方向性

これらの情報から、実際の投資方針を以下のように検討することとします。

1, オッズに応じて投資機会集合の手法でグラフを作成する（単勝、複勝、１〜２番人気のみ）

2, 効率的フロンティア範囲にプラス区間があれば、それの保有割合に応じて投票をする

3, 効率的フロンティア範囲にプラス区間がない場合、期待値に基づいた投票を行い、単勝も複勝も期待リターンが1を下回る場合は投票を行わない。

補足

本来はパドックをみて判断したりすることが望ましいはずです。だが今回はオッズのみを参考に計算することとしました。これはそのパドックでの判断や、それを受けたパドック解説の評価がオッズには反映されているという前提を用いたことによります。穴馬を発見するという手法は獣医学部等のメンバーに聞いてみるのも有効かと思われますが、あくまで経済学部的な視点で実施しました。

実際に競馬場に行ってみた！

ではここからは、実際に競馬場に行って競馬に挑戦してみます。

ここまで「課題設定」「仮説立て」を行ってきました。それらの段階内でも「問い」「仮説」「検証」を行ってきましたが、ここからはそれによってたてられた仮説全体を検証してみるということです。

馬券を購入することについて

この日の軍資金は1万円。他の競馬場で開催されているレースの馬券も購入することができるので、それらも今回の購入対象としました。あるレースの単勝一点に1万円を賭けたりするのも楽しそうではありますが、経済学においては投資で堅く利益を得るにはリスク分散をすることが鉄則と思っていますので、今回はそれに準じてできるだけ多くのレースに少額で賭けることにしました。合計20レースほど賭けたましたが、全体的に賭け方は上で紹介したのと同じなので、一部を抜粋して紹介します。

馬券１

一番人気が3.8倍、二番人気が4.8倍。

期待リターンと標準偏差を求めると、購入比率が1番人気60%、2番人気40%の時に最もばらつきが少なく、期待されるリターンが7.64％と出ました。ここから1番人気の割合を減らせば、期待されるリターンが大きくなっていきます。ここでは50％対50％で買うことにしました。それぞれの単勝に200円ずつ賭けます。

この結果、このレースは2番人気が優勝しました。さらになんと最終オッズが6倍まで膨れていたようで、1200円になりました。ラッキーです。

馬券２

一番人気が3.8倍、4.8倍だったので、馬券１の場合と同様に200円ずつ購入しました。

しかし、このレースでは両方外れてしまいました。このようなハズレもありながら、最終的には期待値あたりに収束していくであろう、ということなのです。いいことばかりではありません。1200円当たったところでやめておけば良かったのかもしれませんね。

馬券３

一番人気が5.7倍、2番人気が5.8倍だったので、同様に計算し単勝を200円ずつ購入しました。またそれらの複勝のオッズも2倍以上あり、計算すると50%対50％で購入した時のリターンがプラスだったので、複勝についても購入しました。その結果、1頭が一位になり、単勝と複勝合わせて1320円のリターンを得ることができました。単勝と複勝はそれぞれ干渉しないため、別々に期待値を計算することとしたのです。

なお、ある馬について単勝と複勝を同時に買うと「応援馬券」と言うようで、馬券の上に「がんばれ！」と表示されるのは面白かったですね。

馬券４？

この日は500円以上馬券を買った人だけが参加できる抽選会なるものが開催されていました。競馬自体が畜産を発展させることなどを意識しているようです。「すき焼き用の高級肉が当たる」という謳い文句を聞き、無料抽選会に参加してみました。すき焼き肉は当たりませんでしたが、飲むヨーグルトのようなものを一ついただいたのでまあ、これも勝ち馬投票券ということで良いでしょう。「競馬場にきている人はこういう抽選とか好きなんだろ！？」みたいな雰囲気を感じて、まんまとやられている感じもしましたが、楽しければ良いのです。

実際に馬券を購入して感じたこと

オッズを掴みにくい

私が考えた賭け方はオッズへの依存度がかなり高いものですが、それゆえに見逃していた欠点がありました。それは締め切り直前にかなりオッズが変化するということです。計算し、マークシートに記入し、購入するプロセスを考えると、遅くとも締め切り5分前くらい時点で参考にするオッズは決めてしまわなければなりません。実際、購入後に最終オッズを見ると人気順が逆転していたりということもありました。策として、期待値系の計算を自動化したりはしてみましたが、それでも最終オッズとズレは生じるのである程度は割り切る必要があると感じました。

しかし見方を変えれば、「やってみないと分からない！」という教訓を得ることができたと言うこともできます。受験生の時も、わかったつもりになっていた問題でも実際に解いてみたら手が止まってしまう、という経験をしたことを思い出しました。

掛け金の割合を調整しにくい

10％対90％などのように、馬券の購入割合を調整しようと思っていましたが、馬券購入の最小単位が100円であることから、1:9にするためには最低でも1000円を使う必要があります。10000円で20レースやろうとしているのに、これでは都合が悪いですね。実際は5:5などの購入に落ち着いてしまうであろうということを感じました。

思わぬ出費

競馬初心者丸出しで恥ずかしいのですが、東京競馬場に入る前に入場料を200円取られることを考慮しそびれていました。競馬場に行くだけで交通費も合わせてマイナススタートであるということを、机上で必勝法を考えるに当たってはつい抜け落ちていたのです。期待リターンから天引きする手法が良いか、と考えたりはしましたが、ややこしくなりそうなのでやめました。これからはネット競馬の時代かもしれません。

最終的なもうけ

この日は軍資金1万円でしたが、ペース配分を間違えた（正確には競馬場グルメを巡っていると、投票予定のレースを逃してしまった）ため、実際の掛け金は8500円でありました。そして、払い戻し金額は8770円でした。すなわち、270円勝ちだったのです！あとはここに飲むヨーグルト1本が入る、といったところでしょうか。

これが多いか少ないか、といえばかなり少ないでしょう。しかし、3%のもうけがでたことは注目すべきです。1週間でJRAの競馬は2日間開催されます。一年間で換算するとおよそ100日間あります。3％の儲けを仮に100日繰り返すと、複利では1.03の100乗で19.2186倍になるのです。3%の儲け分を次また原資としてかけていけば、元手10000円の場合19万2000円ほどになるということです。100万円であれば1900万円ですね。年利1900%の投資商品はなかなか珍しいでしょう。日本国債の利回りが1.5％くらいなので、国債の1200倍くらい儲かるのです。しかし、その分負ける可能性が高く、リターンのばらつきが大きいことは言うまでもありません。

人件費について

だが、賃金についても考慮したい。今回の10000円では270円しか儲かりませんでした。5時間くらいいたので、時給換算だと54円です。東京都の最低賃金が1300円程度であることを考慮すると、1300円×5時間＝6500円相当の儲けを得るためには、利回り3％ならば原資が216,666円必要ということになります。年間で複利を考えると少し数値は変化します。100日×5時間＝500時間で650000円です。19.2倍から元本を引いた数が65万より大きくなるためには、元本が36000円ほどあれば良いので、これなら比較的現実的なラインではありそうですね。

まとめ

今回は東大生が10000円を競馬に投じてみるとどうなるのか、というテーマで紹介してきました。自己を顧みるに、さまざまな観点で一つの対象物を見る、という点が特徴的であろうと思われます。しかし、それらは当然ながら脳の回転が優れているとかそういうことではなく、「問い」「仮説」「検証」のプロセスを行った結果、次々に気になることや観点が生まれてきたということに過ぎません。また、授業などで学んだことをいかに使えるだろうかという姿勢も含まれるでしょう。

日常の生活に少しのマインドセットを組み込めば、意外に世界の見え方は変わるのではないだろうか、という提案として、この記事をしめさせていただきます。最後までご覧いただきありがとうございました。