今回は現役東大生の光永さんにお越しいただきました。彼が高校生のときに面白いと思ったのは「化学基礎の授業」です。最初は苦手だった化学がどんどん楽しくなっていったそうで……。具体的にお話を伺っていきます。
mol(モル)の計算には「図式化」を使う!
坂木:今回は、現役東大生の光永くんに話を聞いてみようと思います。光永さん、あなたが受けてきた授業で面白かったな、わかりやすかったなと思うもので高校生や教員の読者さんに紹介したいものがあれば教えてください!
光永:そうですね、高校1年生の時に受けていた化学基礎の授業で、自分の中に大きな変化がありました。
坂木:ほう、どのような変化ですか?化学というと暗記が多く、最初の方でつまずく生徒さんが多い印象ですが。
光永:私も苦しんでいた一人でした。特にmol(モル)の計算でつまずいていました。molから体積、質量、分子の個数、実際の個数への変換が問われるのですが、よく間違えていました。そこで学校の先生が教えてくれたのが「図式化」です。
坂木:図式化、ですか。
光永:はい、以下のような図を使います。中心となる箱から、三方向に線が伸びていて、そこの関係性を考える、といったものです。坂木さん、中心に入るのはなんだかわかりますか?
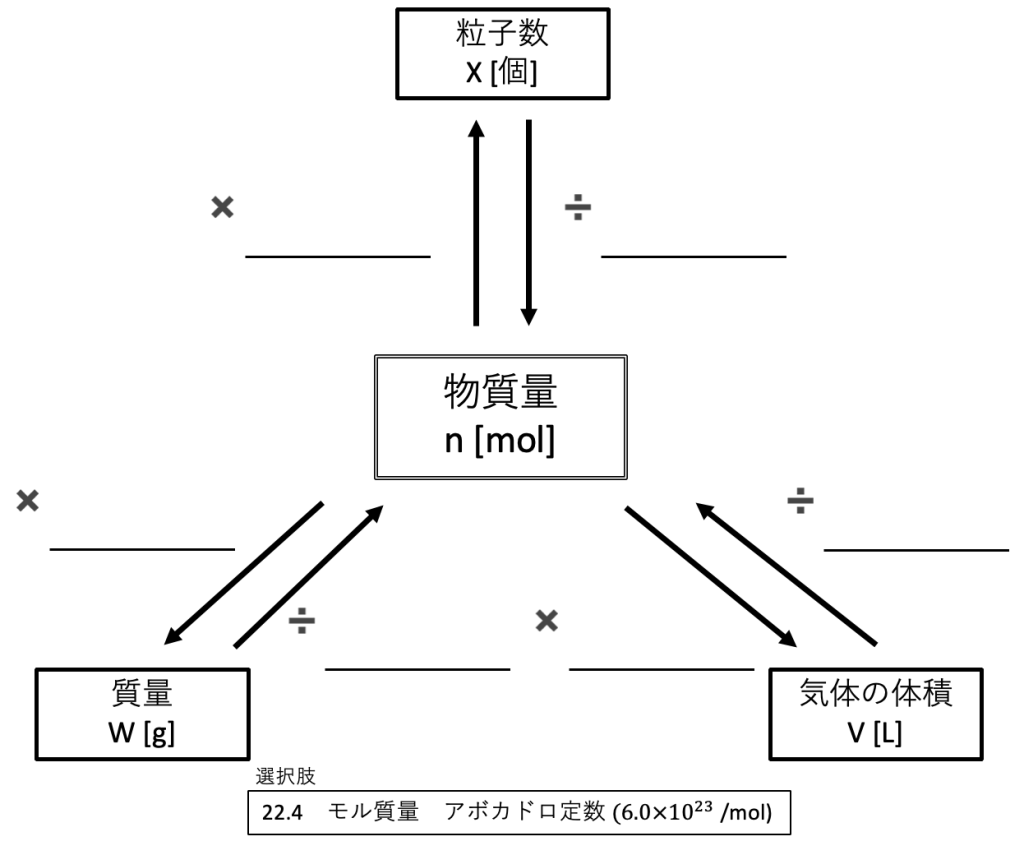
坂木:そうですね、やっぱり一番使うものなのでmol、でしょうか?
光永:正解です。真ん中にmolを書き込んであげて、周りとの関係性を考えてあげます。そもそもmolですが、実生活でいうところの「◯ダース」と同じ考えだと考えるとわかりやすいです。鉛筆を大量に購入したい時に、いちいち何本も買うよりはまとめて3ダース(36本)、4ダース(48本)買った方が楽ですよね?私たちは何ダースかと言われたら、1ダースは12個なので自ずと個数も求められます。
坂木:確かにそうですね。それとmolとはどんな関係があるんですか?
光永:molもダースと同じ概念なんです!考えてみてください、分子はとても小さく、後で説明しますが例えば鉄55.85gになんと6.02×10²³個もの原子が含まれています。実験で測定するときなど、毎回分子や原子の個数で計算していたらキリがないですよね?そこで出たのがmolの概念です。1mol=6.02×10²³ とし、この右辺の数をアボガドロ定数と定義したわけです。
さて、実際に空欄を埋めていきましょう。 まず「実際の個数」ですね。ここは先ほどの話からわかると思います。
坂木:molの数にアボガドロ定数をかけてあげればいい、ってことですよね?
光永:そうです!逆に「実際の個数」から「mol」への変換をした場合は、アボガドロ定数で割ればいい、ということです。
次は質量にいきましょうか。質量とは、その分子、原子の重さに左右されますね。例えば炭素と鉄では同じ1個の原子でも、その質量には差があります。
光永:ここに元素の周期表がありますが、原子番号が大きくなるほど一個の原子あたりの質量も大きくなっていますね。ここで大事になってくるのが「モル質量」です。モル質量とは、1molあたりどれくらいの質量を持っているか、という物質固有の値です。これを原子なら「原子量」、分子なら「分子量」と呼んだりします。
先ほどの鉄なら原子量が55.85なので、1molあたりの質量が1×55.85=55.85gとなるわけです。
坂木:なるほど、それでは体積は?
光永:体積は、気体の場合、標準状態(0℃、1気圧)では1molあたり22.4Lですので、「mol」から「体積」への変換の時には22.4をかけてあげればよく、逆の際は割ればいいということです。
さて、これである程度の基礎はできました。
問題を解いてみよう!
実際の問題では、
①何を求めればいいのか
②そのために必要な値はなにか(分子量など)
③計算をする という流れで解くことができます。
光永:例えば以下のような問題はどのように解くのでしょうか?
問題
標準状態で44.8Lの二酸化炭素CO₂は何gか。ただし、C=12、O=16とする。
坂木:うーん、まずは何を求めればいいか、ですよね。質量を求める問題なので、molから質量への変換が必要そうです。
光永:その通りです!まず体積からmolを求めて、そこから質量に変換すればいいわけです。順を追って見ていきましょう。
まず、44.8Lの気体が何molかを求めます。1mol=22.4Lなので、 44.8÷22.4=2mol
次に、CO₂の分子量を求めます。C=12、O=16なので、 CO₂の分子量=12+16×2=44
最後に、molから質量への変換です。モル質量が44g/molなので、 2mol×44g/mol=88g
答えは88gとなります。
坂木:なるほど!図を頭に思い浮かべながら、molを中心に段階的に変換していけばいいんですね。
光永:そうなんです。この図式化の良いところは、どの値からスタートしても、一度molに戻してから目的の値に変換すればいい、というルートが明確になることです。質量→体積の変換も、質量→mol→体積という流れで考えれば混乱しません。
坂木:確かに、暗記ではなく「理解」して使える知識になりますね。この授業を受けて、光永さんの化学への取り組み方は変わりましたか?
光永:大きく変わりました。それまでは公式を丸暗記して、どの問題にどの公式を使うか、という機械的な解き方をしていました。この図式化を学んでからは、mol計算の全体像が見えるようになって、自信を持って問題に取り組めるようになりました。暗記に頼らず、理解して解けるようになったんです。
この考え方は化学の他の分野でも応用できます。化学反応式の量的関係を考える時も、常にmolを基準に考える癖がついたので、複雑な問題でも整理しやすくなりました。
坂木:素晴らしいですね。図式化によって、単なる暗記から概念の理解へとシフトできたわけですね。最後に、この学習法をどんな生徒さんにおすすめしたいですか?
光永:mol計算でつまずいている生徒さんには、ぜひ試してほしいです。特に「公式が多すぎて覚えられない」「どの公式を使えばいいかわからない」と悩んでいる人には効果的だと思います。図を一つ覚えるだけで、すべての変換の関係性が頭に入るので、暗記の負担が大幅に減ります。
それと、化学が苦手だと思っている生徒さんにも試してほしいです。私自身がそうだったように、理解できると化学が楽しくなります。一つの分野が得意になると、他の分野への自信にもつながりますから。
万能テクニックの「図式化」 世界史で光る真価とは
坂木:mol計算を図式化することで全体像を掴み、暗記ではなく理解に基づいた学習ができるようになる。まさに「わかる」から「できる」への転換ですね。化学でつまずいている生徒さんや、より効果的な教え方を探している先生方にとって、とても参考になるお話でした。この「図式化」という作業は、他の科目でも使えそうですね。
光永:その通りです。実際、この図式化を世界史でも活用することで深い理解を得ることができました。世界史の教科書では、中世と近世の時代の間にアジア史やヨーロッパ史を挟むことがあります。勉強している身としては、中世から近世へのつながりがわからないのです。
時代が移り変わるということは、そこで様々な事象が起きたはずなのに、理解が深まらないことが多いのです。勉強しながら一つの問いが生まれました。「中世から近世にかけて、どのような変化があったのだろうか」、という疑問です。
そこで用いたのが「図式化」です。2つの教科書を並べ、中世後期から近世に起きた事柄を書き出し、それらの関係性を因果関係などを考えることにより図式化していきます。当時のノートを再現したものが以下です。

光永:このようにまとめてみることにより、時代の転換期には、宗教改革が強く影響していたこと、またその改革がなぜ起こったのか、などの史実を連続性があるものとして理解することができます。
坂木:とても興味深い勉強法ですね。自分の言葉、図式でまとめることのメリットはやはり「記憶に残る」ことですか?
光永:それもありますが、他にも効果はあります。このように図式化することにより、普段では見逃すような「問い」を深ぼることができます。深ぼる過程で新しい知識のピースを得たり、逆に新しい他の問いが出てくることがあります。そのように問いを深ぼり、自分の中で一つの問いに対する仮説を作ることで、論理的な思考力が身につきます。
この能力は、ただ目の前の図式を綺麗に作るために使われるのではなく、受験本番でもとても役に立ちます。実際、東大をはじめとする世界史の問題では、知識自体を問われるのではなく、その知識をどう使うかというのが重要視されます。この思考力を鍛える一歩として、図式化はとてもクリティカルな勉強法だと信じています。
坂木:光永さん、ありがとうございました。情報に囲まれる現代において、このように自分で整理する力はとても大事だなと感じます。ただ受動的に知識を聞くのではなく、主体的に手と頭を動かし、自分の中の解釈を作り、時にはその解釈が破壊され次なるブレイクスルーが起きていく。そのようにして勉強をしている人が今後はこと受験だけではなく長い人生においても勝ち続けるのではと思わされる内容でした。
是非このような「図式化」する練習を、学校の現場でも取り入れてみてはいかがでしょうか。そのきっかけの一つに化学のmol学習で用いてみるのもいいですね。
東大生が面白いと思った授業「mol(モル)を図式化しよう!」
印刷して使えるPDF資料を配布中!ぜひ授業でご活用ください!
公式サイトにて、カルぺ・ディエムが提供している具体的なサービスを紹介中!
カルペ・ディエムでは、学校や保護者のみなさまが抱える懸念やニーズに応える形で、講演・講座・ワークショップを提案し、それらを実施しております。
生徒の皆さんの大学選びや学部選びのワークショップ、モチベーション向上を目的とした講演、独自の探究学習授業、長期休暇中の学習合宿、難関大学合格を目指した通年プロジェクトなど、さまざまなプランをご用意しております。
私たちの講師は現役東大生で 偏差値35から東大合格を果たした西岡壱誠をはじめ、地域格差や経済格差などの多様な逆境を乗り越えた講師たちが、生徒の皆さんに寄り添って全力でサポートいたします。
ご質問やご相談だけでも結構ですので、お気軽にお問い合わせください。


















