モンティホール問題って何?
みなさんは、テレビのクイズ番組に出場しているところを想像してみてください。目の前には3つのドアがあり、そのうち1つには豪華な賞品、残り2つにはハズレが隠されています。司会者は言います。
「好きなドアを1つ選んでください。ただし、まだ開けてはいけません。」
あなたは、ドアAを選びました。すると司会者が言いました。
「では、あなたが選ばなかった2つのうち、1つハズレのドアを開けましょう。」
司会者はドアCを開け、そこにはハズレがありました。そして彼はこう言います。
「ここでチャンスです。今なら、最初に選んだドアAをそのままにするか、手付かずのドアBに変更するかを選べます。さあ、どちらにしますか?」
さて、ここで問題です。
ドアを変更した方が良いのでしょうか?それとも、どちらを選んでも同じなのでしょうか?
この問題は、モンティ・ホール問題と呼ばれています。アメリカのゲーム番組『Let’s Make a Deal』で司会を務めたモンティ・ホール氏にちなんで名付けられました。この問題自体は簡単な設定なのに答えは直感に反することから、人々を混乱させ、アメリカ国内で大きな波乱を呼びました。
今回は、この不思議な問題を通して確率とは何かを一緒に考えていきましょう。
多くの人が間違える理由
さて、さっきの質問に皆さんはどう答えたでしょうか。「ドアを変えても、変えなくても、当たる確率はどちらも1/2なんじゃない?」と思いませんでしたか?直感ではこのように考えてしまう人も多そうです。
なぜなら、ドアCが開いた後に、残るドアは2つだけ。直感的には「ドアAとドアBのどちらを選んでも確率は1/2っぽい」と感じますよね。でも、これは「直感に頼った思い込み」であり、間違っているんです。
このモンティ・ホール問題は、1990年代にアメリカの雑誌で取り上げられ、全国で大論争を巻き起こしました。なんと、数学の先生や大学教授までもが間違った回答をしてしまったのです。
なぜこんなに多くの人が間違えるのでしょうか?それは「状況が変化していること」に気づかず、単純に「残り2つだから半々」と考えてしまうからです。実は、司会者が「わざとハズレのドアを開ける」という行動が、大きなヒントになっているのです。
このように、私たちは確率の問題で「直感」や「イメージ」に頼りがち。でも数学的に正しく考えるためには、状況を論理的に整理し直すことが大切です。
実はこう考える!正解とその理由
さて、結論から言うと、「ドアを変更した方が当たる確率は高くなります」。具体的には、
つまり、ドアを変更すれば、当たる確率は2倍になるのです!
「えっ、なんでそんなことになるの?」と不思議に思いますよね。そこで、状況を少し整理してみましょう。
まず、最初にドアを選ぶ段階では、当たりは3つのうち1つ。
つまり、あなたが最初に選んだドアが当たりである確率は1/3です。そして、残りの2つのドアのどちらかに当たりがある確率は2/3です。
ここで司会者が登場し、あなたが選ばなかった2つのうちハズレであるドアを必ず開けてくれます。つまり、残った1つのドアは、もともと2/3の確率で「当たり」だった2つのドアのうちの片方なのです。ハズレが除かれたことで、その「当たりの可能性」が1つのドアに集まった、ということになります。
もう少しイメージしやすくするために、極端な例を考えてみましょう。もしドアが100個あって、あなたが1つを選んだとします。残りの99個のうち、司会者が98個のハズレを開けて、1つだけドアを残したらどうでしょう?最初に選んだ1つのドアが当たりである確率は1/100。残った1つのドアが当たりである確率は、なんと99/100!
これなら、「変更した方がいい」と納得しやすいですよね。
本当に正しい? 実験してみよう!
「理屈はわかったけど、本当にそうなるの?」と感じた人もいるかもしれません。そんなときは、実験してみるのが一番! 紙コップと消しゴムがあれば、友達と一緒に簡単にシミュレーションができます。
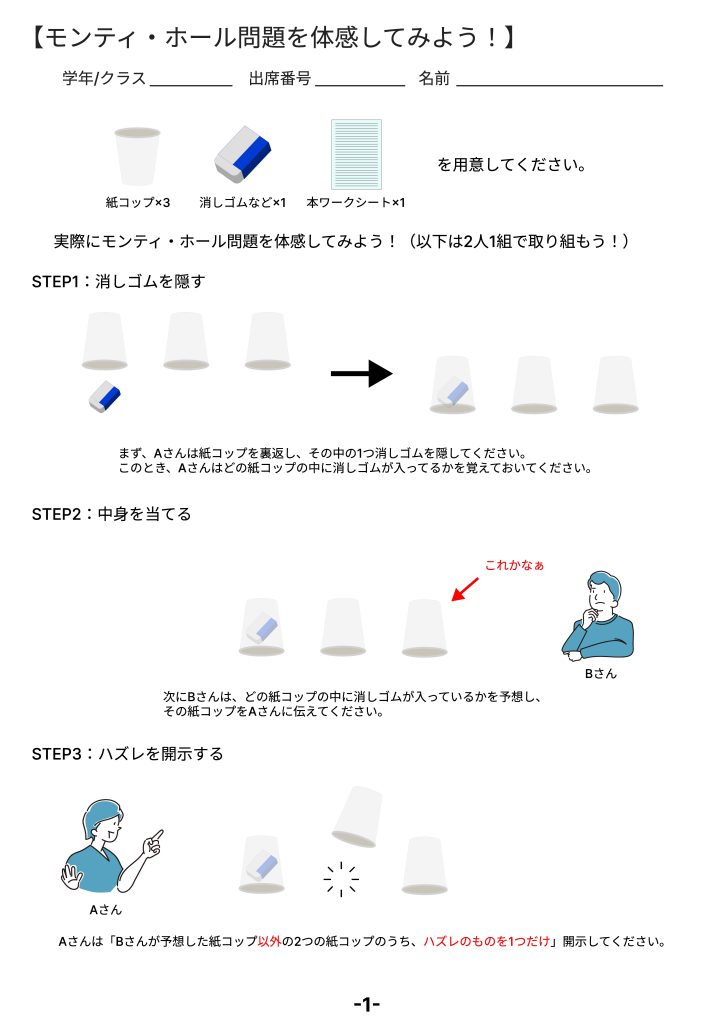
紙コップを3つ用意し、そのうちの1つに消しゴムを隠してください。
プレイヤー役の人は、どの紙コップの中に消しゴムが入っているかを予想し、司会者役の人に伝えてください。
司会者役の人は、「プレイヤー役の人が予想した紙コップ以外の2つの紙コップのうち、ハズレのものを1つだけ」開示してください。
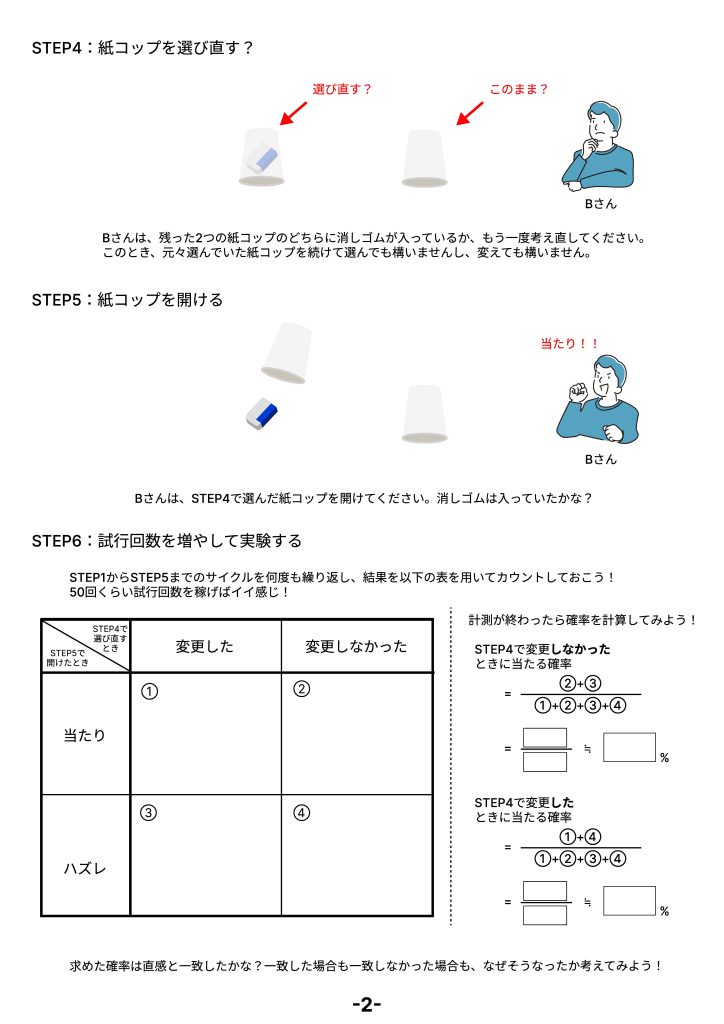
プレイヤー役の人は、残った2つの紙コップのどちらに消しゴムが入っているか、もう一度考え直してください。
プレイヤー役の人は、STEP4で選んだ紙コップを開けてください。消しゴムは入っていたかな?
これを50回ずつくらい繰り返して、「変更した場合」と「変更しなかった場合」の当選率を比べてみてください。
実際にやってみると、変更した方が明らかに当たる確率が高いことがわかります。100回のうち、変更した人はだいたい66回くらい当たり、変更しなかった人は33回程度しか当たりません。
モンティ・ホール問題の演習に使えるワークシートを無料で配布中です。
普段の学習に、授業に、ぜひご利用ください!
日常生活にもある!?モンティホール的な選択
モンティ。ホール問題は一見特殊なゲームの話のように思えますが、実は私たちの日常生活にも似たようなシチュエーションがたくさんあります。
例えば、あなたが模試の自己採点をしていて、答えに自信がない問題を見直しているとします。「この選択肢、なんとなく違う気がするけど…変えた方がいいかな?」という場面。これは「情報が増えたあとに、初めの選択を見直す」という点で、モンティ・ホール問題にとても似ています。
また、買い物をするとき、安いけど低品質の商品Aと高いけど高品質の商品Bで悩んでいて、いざAを買うぞ!と決めた後に「今ならBは割引中ですよ(ただし、Aよりは高いまま)」という情報が入ってくるとします。こうしたときに、「Aを買い続けるか」「新しい情報を活かしてBを買うか」という判断も、同じような構造を持っています。
人はしばしば「最初に選んだもの」に愛着を持ちすぎてしまう傾向があります。これは保有効果と呼ばれる心理的なバイアスなんです。
おわりに
数学は、ただ計算するだけでなく、「ものごとをどう考えるか」を学ぶ学問です。モンティ・ホール問題は、「直感に反するけれど正しい」答えを通して、論理的思考の面白さを教えてくれます。
あなたも、次に選択を迫られたとき、「今、自分の判断は論理的かな?」と少しだけ立ち止まってみると、新しい発見があるかもしれませんよ。
また、モンティ・ホール問題の奥には、条件付き確率やベイズの定理といった、もっと高度な確率の考え方が隠れています。これらは高校や大学で学ぶ数学につながる重要なトピックです。興味がある人は、そのようなトピックで検索してみると、さらに学びが深まりますよ!
公式サイトにて、カルぺ・ディエムが提供している具体的なサービスを紹介中!
カルペ・ディエムでは、学校や保護者のみなさまが抱える懸念やニーズに応える形で、講演・講座・ワークショップを提案し、それらを実施しております。
生徒の皆さんの大学選びや学部選びのワークショップ、モチベーション向上を目的とした講演、独自の探究学習授業、長期休暇中の学習合宿、難関大学合格を目指した通年プロジェクトなど、さまざまなプランをご用意しております。
私たちの講師は現役東大生で 偏差値35から東大合格を果たした西岡壱誠をはじめ、地域格差や経済格差などの多様な逆境を乗り越えた講師たちが、生徒の皆さんに寄り添って全力でサポートいたします。
ご質問やご相談だけでも結構ですので、お気軽にお問い合わせください。